
Zadanie Najlżejszy język (naj)
Pomóż nam usprawnić bazę zadań!
The Lightest Language
Memory limit: 32 MB
Alphabet 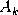 consists of
consists of 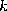 initial letters of English alphabet.
A positive integer called a weight is assigned to each letter of the alphabet.
A weight of a word built from the letters of the alphabet
initial letters of English alphabet.
A positive integer called a weight is assigned to each letter of the alphabet.
A weight of a word built from the letters of the alphabet 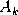 is the sum of weights of all letters in this word.
A language over an alphabet
is the sum of weights of all letters in this word.
A language over an alphabet 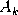 is any finite set of words built from the letters of this alphabet.
A weight of a language is the sum of weights of all its words.
is any finite set of words built from the letters of this alphabet.
A weight of a language is the sum of weights of all its words.
We say that the language is prefixless if for each pair of different words 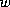 ,
,  from this language
from this language 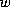 is not a prefix of
is not a prefix of  .
We want to find out what is the minimal possible weight of an
.
We want to find out what is the minimal possible weight of an  -element, prefixless language over an alphabet
-element, prefixless language over an alphabet 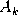 .
.
Example
Assume that 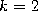 , the weight of the letter
, the weight of the letter  —
— 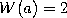 and
the weight of the letter
and
the weight of the letter 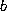 —
— 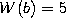 .
Then the weight of the word
.
Then the weight of the word 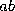 —
— 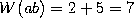 .
. 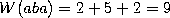 .
The weight of the language
.
The weight of the language 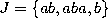 —
— 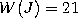 .
The language
.
The language 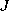 is not prefixless, since the word
is not prefixless, since the word 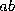 is a prefix of
is a prefix of 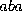 .
The lightest tree-element, prefixless language over the alphabet
.
The lightest tree-element, prefixless language over the alphabet 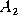 (assuming that weights of the letters are as before) is
(assuming that weights of the letters are as before) is 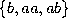 ; its weight is
; its weight is 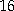 .
.
Task
Write a program that:
- reads two integers
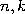 and the weights of
and the weights of 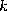 letters of an alphabet
letters of an alphabet 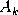 from the standard input;
from the standard input;
- computes the minimal weight of a prefixless,
 -element language over the alphabet
-element language over the alphabet 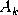 ;
;
- writes the result to the standard output.
Input
In the first line of the standard input there are two positive integers  and
and 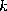 separated by a single space, (
separated by a single space, (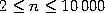 ,
, 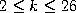 ).
These are the number of words in a language and the number of letters in an alphabet respectively.
The second line contains
).
These are the number of words in a language and the number of letters in an alphabet respectively.
The second line contains 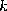 positive integers separated by single spaces.
Each of them is not greater than
positive integers separated by single spaces.
Each of them is not greater than 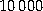 .
The
.
The 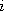 -th number is the weight of the
-th number is the weight of the 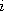 -th letter.
-th letter.
Output
In the first and only line of the standard output there should be written one integer —
the weight of the lightest prefixless  -element language over the alphabet
-element language over the alphabet 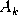 .
.
Example
For the input data:
3 2 2 5
the correct result is:
16
Task author: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English